翻页效果模拟
效果展示
这是一个简单的翻页模拟,还是大学里面研究的,这里相当于是复习一下,所以准备重新梳理一下文章。
绘制准备
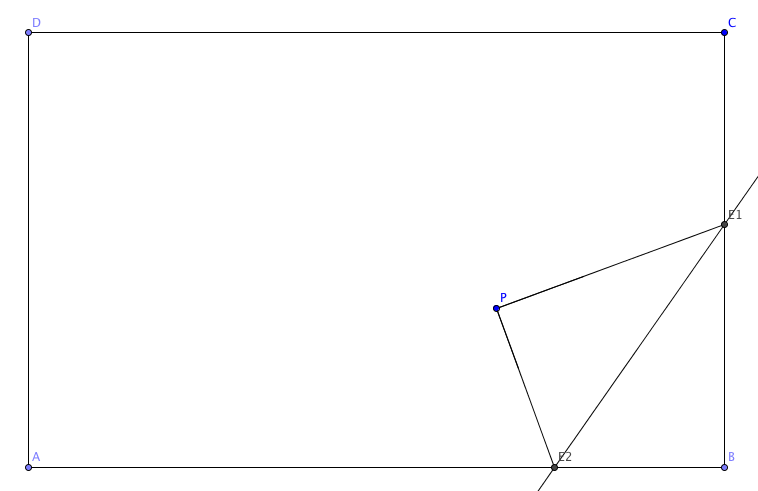
- 这里为了简单体检,我使用的是
GeoGebra进行模拟,在画布上绘制一个矩形ABCD, 然后新建一个点P, 相当于我们的手指触摸; - 然后做点P和点B的中垂线与矩形的边AB和边BC分别相交与E2,E1点:
计算弯曲点
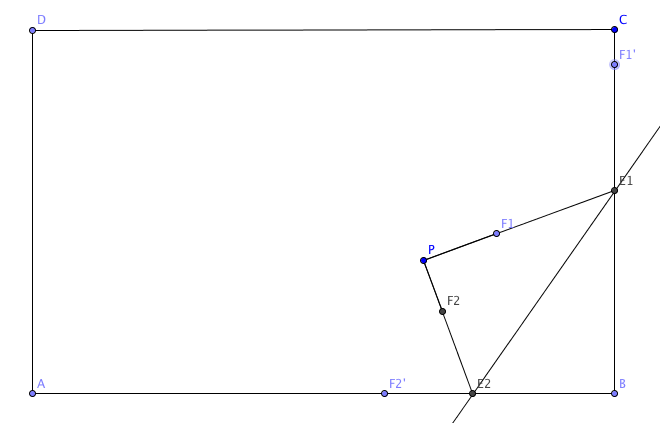
假设我们对纸张没有任何的弯曲, 那么线段E1E2就是折痕,但是大自然是很神奇的,纸张反抗,会有一些弯曲,先不关注怎么弯曲的,
纸张一定有一段是直的,没有弯曲,我们以线段PF2为例子,假设弯曲部分比例是 $f\in (0,1]$. 所以我们可以在线段PE2上面作点F2使|PF2|=f|PE2|.
所以这里的点命令为:F2=(1-f)P+E2,同理,做出线段PF1上的点F1. 这里我们可以认为点F1和点F2是纸张的完全开始点,那么物理上,
肯定在线段AB和BC上面存在与之对应的点,并且弯曲部分的曲线也一定是对称的,一样,以F2为例子,那么点F2’的坐标可以表示为((x(E2)-|F2E2|,0),
曲线如下:
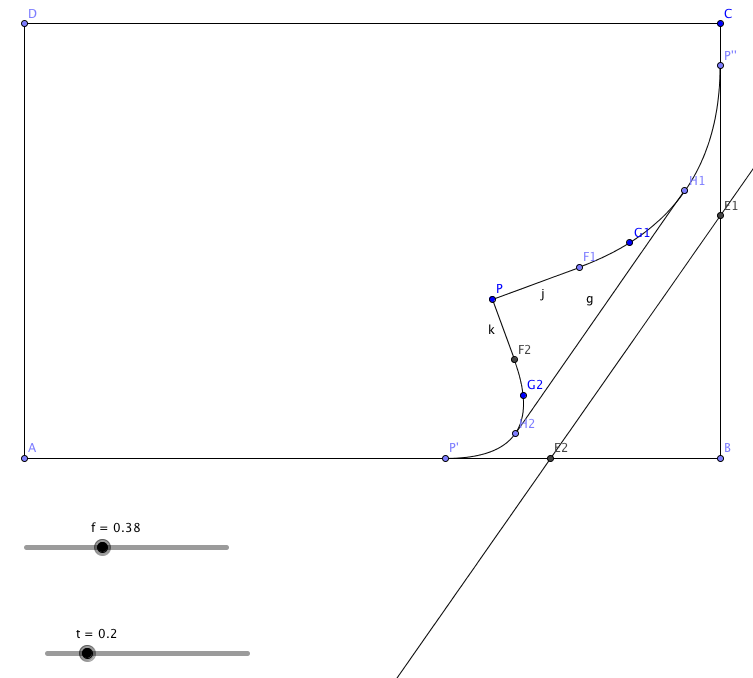
绘制弯曲部分曲线
这里的曲线是贝塞尔曲线,并且它的三个控制点我们都已经找出来了,分辨是折点、弯曲点和对称的弯曲点,这里我们去除掉线段PE2和线段PE1,然后根据三个控制点绘制贝塞尔曲线。这里有一点需要注意,Geogebra并没有自带贝塞尔曲线的函数,所以我们需要借助轨迹功能,来绘制函数的轨迹,这就要求我们清楚贝塞尔的定义:
线性贝塞尔曲线
给定点P0、P1,线性贝塞尔曲线只是一条两点之间的直线。这条线由下式给出: \(B(t) = { P }_{ 0 }+t({ P }_{ 1 }-{ P }_{ 0 })=(1-t){ P }_{ 0 }+t{ P }_{ 1 }\quad ,t\in [0,1]\) 且其等同于线性插值。
线性贝塞尔曲线函数中的t会经过由P0至P1的B(t)所描述的曲线。例如当t=0.25时,B(t)即一条由点P0至P1路径的四分之一处。就像由0至1的连续t,B(t)描述一条由P0至P1的直线。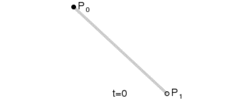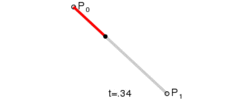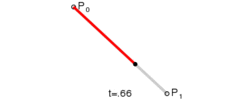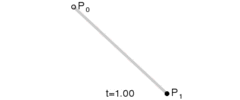
二次方贝塞尔曲线
二次相当于是对一次的扩充
二次方贝塞尔曲线的路径由给定点P0、P1、P2的函数B(t)追踪: \(B(t)={ (1-t) }^{ 2 }{ P }_{ 0 }+2t(1-t){ P }_{ 1 }+{ t }^{ 2 }{ P }_{ 2 }\quad ,t\in [0,1]\) TrueType字型就运用了以贝塞尔样条组成的二次贝塞尔曲线。
为建构二次贝塞尔曲线,可以中介点Q0和Q1作为由0至1的t:
由P0至P1的连续点Q0,描述一条线性贝塞尔曲线。 由P1至P2的连续点Q1,描述一条线性贝塞尔曲线。 由Q0至Q1的连续点B(t),描述一条二次贝塞尔曲线。
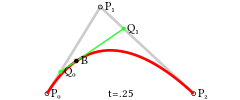
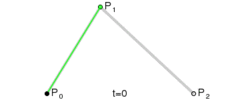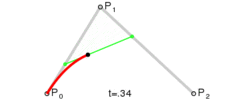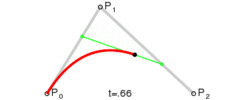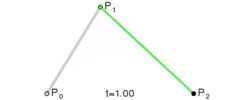
所以我们的F2-E2-F2’上的贝塞尔轨迹可以表示为$B(t)=(1-t)((1-t)F2+tE2)+t((1-t)E2+tF2’)\quad ,t\in[0,1]$,作图如下:
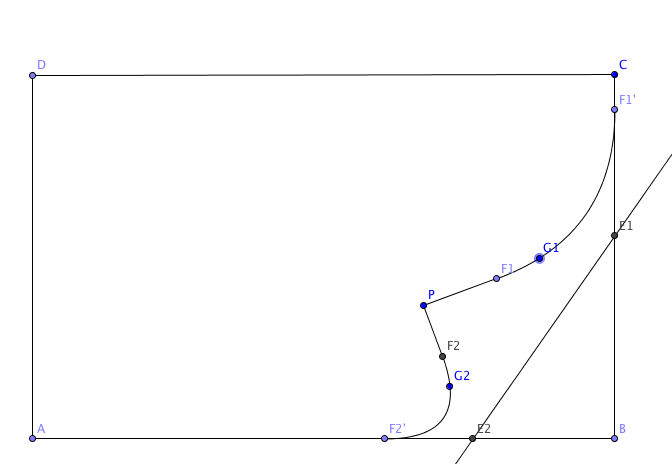
绘制弯曲部分的切线
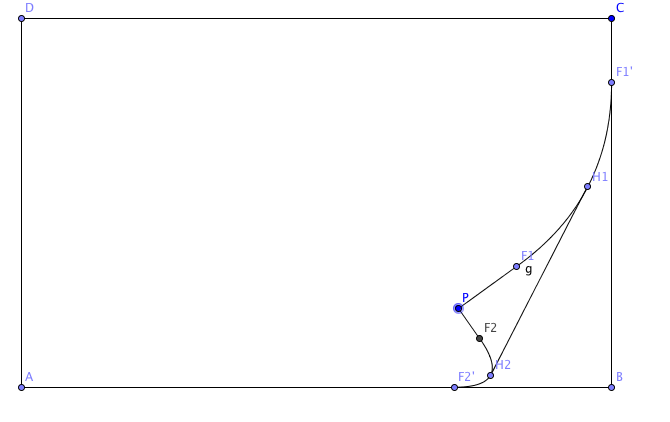
到这里,应该是已经完成了纸张弯曲的模拟部分了,但是为了更加接近于纸张的效果,我们需要作弯曲部分的切线,这个我也是想了很长时间,可以这样简单理解,我弯曲纸张,那么弯曲上下两部分收到的作用应该是一样的,所以弯曲的曲线一定是对称的,那么我们的切点其实就是曲线的中点。而一次贝塞尔曲线的中点很简单,就是两个点相加除以2的问题,那么二次呢?我们知道二次是对一次的扩充,所以我们相当于先对两个一次贝塞尔曲线求中点,然后再对中点连成的曲线求中点, $B(t)=(1-t)((1-t)F2+tE2)+t((1-t)E2+tF2’) ,t=\frac { 1 }{ 2 } $, 最后的效果如下:
工程化
之前尝试过载Android和Qt两个平台上进行编码,Android基本实现了Demo,但是性能非常成问题,所以这里留个任务,之后改进一下计算方法,对理论的计算工程化,争取做一个有意思的Demo出来。